[paper-review] AlignDiff: Aligning Diverse Human Preferences via Behavior-customisable Diffusion Model
Arxiv 2023. [Paper] [Project Page] [Github]
Zibin Dong1, Yifu Yuan1, Jianye Hao†1, Fei Ni1, Yao Mu3, Yan Zheng1, Yujing Hu2, Tangjie Lv2 , Changjie Fan2, Zhipeng Hu2 > 1College of Intelligence and Computing, Tianjin University, 2Fuxi AI Lab, Netease, Inc., Hangzhou, China, 3The University of Hong Kong
3 Oct 2023
한 문장 요약
요약: Human preference를 RLHF로 quantify 하였고, 이를 diffusion 모델로 잘 포착해보자.
Keyword: Abstractness, Mutability
Abstract
Human preference를 RL에서 수행해왔지만, Abstractness, Mutability를 해석하는 것이 어려웠음.
- 저자는 Abstractness를 RLHF로 해결하고,
- Multi-Prospective Human Feedback Dataset을 crowdsourcing으로 구함. 이 데이터셋을 기반으로 Attribute strength를 예측하는 모델을 학습함.
- Mutability를 Guide-Diffusion model로 해결하려 함.
- 1.에서 학습을 통해 구한 Attribute를 condition으로 한 diffusion model을 선보임.
용어 설명
- Abstractness: Relative behavioral attributes 논문에서 소개된 내용. Human preference의 추상적인 의미를 뜻하며, 이를 attribute라는 것으로 정량화 함. 좀 더 자세히 설명하면, Trajectory의 sequence를 기반으로 Behavior Attribute를 정량화 함 (=relative attribute strength).
- 여기서 Behavior Attribute는 PBL에서 수행되던 feature vector와 유사한 의미를 가짐.
- ex) Speed, Jump height, Torso height, Stride length
- In the paper Relative behavioral attributes (ICLR, 2023);
We introduce the notion of Relative Behavioral Attributes (RBA) to capture the relative strength of some properties’ presence in the agent’s behavior. We aim to learn an attribute-parameterized reward function that can encode complex task knowledge while allowing end users to freely increase or decrease the strength of certain behavioral attributes such as “step size” and “movement softness”
- 여기서 Behavior Attribute는 PBL에서 수행되던 feature vector와 유사한 의미를 가짐.
- Mutability: preference가 개개인별로 다르며, 시간에 따라 변화한다는 것을 의미함.
- In the paper IMITATING HUMAN BEHAVIOUR WITH DIFFUSION MODELS (ICLR, 2023);
- CLASSIFIER-FREE GUIDANCE에 대해 varying guidance strengths에 따른 분포의 변화를 보여주는 논문.
- Diffusion-X / Diffusion-KDE 모델을 소개함.
- CLASSIFIER-FREE GUIDANCE에 대해 varying guidance strengths에 따른 분포의 변화를 보여주는 논문.
- In the paper IMITATING HUMAN BEHAVIOUR WITH DIFFUSION MODELS (ICLR, 2023);
Introduction
- Abstractness: Relative Behavioral Attribute (RBA)를 통해 attribute(=preference feature)에 대해 추정할 수 있지만, 이는 single-step state-action에 대한 근시안적인(myopic) 한계를 보여준다.
- Trajectory 전반적으로 잘 해석할 수 있어야 한다. → 1) RLHF로 Dataset을 relabelling 하였으며, → 2) Transformer-based attribute strength model을 제안함.
- Mutability: 사용자의 preference를 잘 포착하더라도, 이러한 preference는 일시적이지 않다. 기존의 방법에 대해서는 매번 Reward fine-tuning을 수행해주어야 하는 치명적인 단점이 존재한다.
- Retraining을 없애자. → Diffusion model
- Agent의 preference matching / switching / covering capability를 평가하기 위한 Metric을 제시함.
- Mean Absolute Error(MAE) between the evaluated and target relative strength
Related Works
- RLHF
- 기존의 RLHF는 single objective를 최적화 하는 것에 초점이 이루어짐.
- RBA는 attribute-conditioned reward model로 human preference를 distill 하는 시도를 보임.
- 다만 이는 Single-step에 대한 것이므로 전반적인 trajectory에 대해서 충분히 고려하지 못함.
- 새로운 preference에 대해 매번 retraining이 필수적임.
- Diffusion Models for Decision-Making
- Reward(or auxiliary information) conditioned 하여 decision trajectory를 생성하는 시도가 이루어졌음.
- 그러나 이는 학습된 분포 내에서 한정적인 부분에 대해서만 생성이 가능했음.
- 학습된 분포에 대해 전반적으로 잘 활용할 수 있게 해보자.
Preliminaries
- Problem Setup
- \[\mathcal{M}=<\mathrm{S,~A,~P~,\alpha}>\]
- \(\mathrm{S}:\) Set of states
- \(\mathrm{A}\): Set of actions
- \(\mathrm{P}: \mathrm{S\times A\times S}~\rightarrow~[0,1]\): Transition function
- \(\mathrm{\alpha}=\{\alpha_{1},\cdots,\alpha_{k}\}\): a set of k predefined attributes used to characterize the agent’s behavior
- 기 정의된 attribute에 대한 내용: ex) Speed, Jump height, Torso height, Stride length
- \(\mathrm{\tau}^{l}=\{s_{0},\cdots,s_{l-1} \}\): length l의 길이만큼 state \(s\)를 갖는 궤적에 대한 표현.
- \(\zeta^{\alpha}(\tau^{l})=\boldsymbol{v}^{\alpha}=[v^{\alpha_{1}},\cdots,v^{\alpha_{k}}]\in [0,1]^{k}\): 궤적을 입력으로 받아, 해당 궤적이 각 attribute에 대해 얼마 만큼의 값을 가지는지 mapping 해주는 함수.
- \(v^{\alpha_{i}}\)의 값이 클 수록 해당 Attribute \(\alpha_{i}\)를 잘 표방한다는 것이며, 작을 수록 그 반대의 의미.
- 저자는 Human preference를 \((\boldsymbol{v^{\alpha}}_{\text{targ}},\boldsymbol{m}^{\alpha})\)의 쌍으로 정의함.
- \(\boldsymbol{v^{\alpha}}_{\text{targ}}\): relative strength를 의미함.
- \(\boldsymbol{m}^{\alpha}\in\{0,1\}^{k}\): binary masking 값을 의미함. 즉, 해당하는 interest of attribute를 뜻함.
- Objective
- find a policy \(a=\pi(\mathrm{s}|\boldsymbol{v^{\alpha}}_{\text{targ}},\boldsymbol{m^{\alpha}})\) that minimizes the L1 norm \(||(\boldsymbol{v^{\alpha}}_{\text{targ}}-\zeta^{\boldsymbol{\alpha}}(\mathop{\mathbb{E}_{\pi}}[\tau^{l}]))~\circ~\boldsymbol{m^{\alpha}}||_{1}\)
- \[\mathcal{M}=<\mathrm{S,~A,~P~,\alpha}>\]
- PbRL
- Bradley-Terry objective에 대한 서술.
- DDIM, Classifier-free Guidance (CFG)
- DDIM, CFG에 대한 일반적인 서술.
- 한 줄 요약:
- We learn human preferences from an unlabeled state-action dataset \(D=\{\tau\}\), which contains multiple behaviors.
Methodology
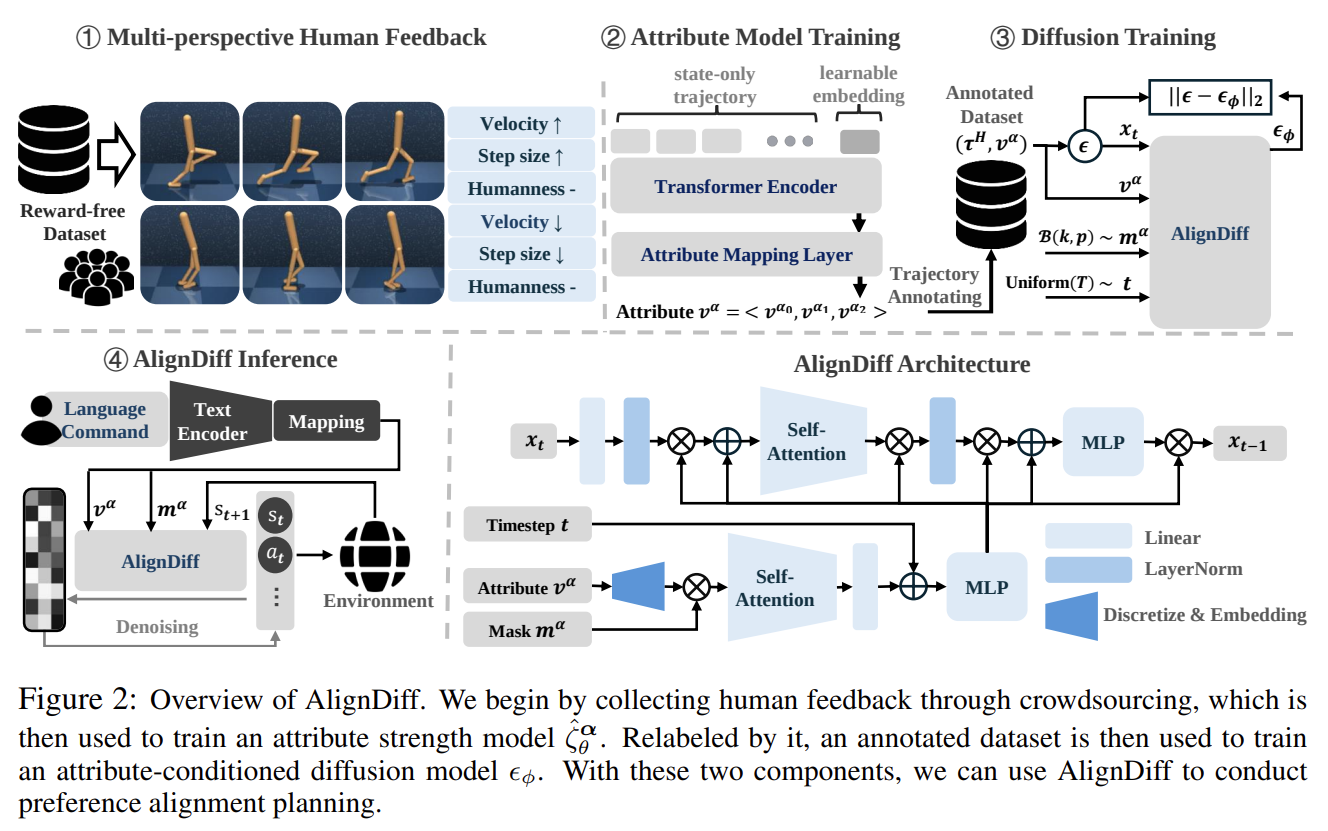
Overall framework of AlignDiff.
저자가 제안하는 방법론 AilgnDiff는 총 4개의 파트로 이루어짐.
- RLHF Dataset: multi-prospective human feedback through crowdsourcing.
- \(D\): Dataset → \(D_{p}=\{(\tau_{1},\tau_{2},y_{\text{attr}})\}, y_{\text{attr}}=(y_{1},\cdots,y_{k})\)
- Train an attribute strength model, which we then use to relabel the behavioral datasets.
- \(D_{G}\): Annotated dataset
- Train a diffusion model with an annotated dataset
- which can understand and generate trajectories with various attributes.
- AlignDiff for inference, aligning agent behaviors with human preferences at any time.
각 파트를 정리하면,
- Multi-Perspective Human Feedback Collection
- Trajectory dataset \(D\)로부터 2개의 pair 궤적 \(\{(\tau_{1}, \tau_{2})\}\)을 사람들에게 각 attribute에 대해서 어떠한 궤적이 더 적합한지 물어본다.
- feedback dataset \(D_{p}=\{(\tau_{1},\tau_{2},y_{\text{attr}})\}\)을 얻는다. Attribute의 예시로는 \((\text{speed, stride, humanness})\) 등이 있다.
- Trajectory dataset \(D\)로부터 2개의 pair 궤적 \(\{(\tau_{1}, \tau_{2})\}\)을 사람들에게 각 attribute에 대해서 어떠한 궤적이 더 적합한지 물어본다.
-
Attribute Strength Model Training
- 저자는 Bradley-Terry objective를 수정하여 제시함.
- 기존의 수식에서 달라진 점은 reward(=feature) mapping function 뿐이다.
- \(r(\xi(\tau_1))\) → \(\hat{\zeta}^{\boldsymbol{\alpha}}_{\theta,i}(\tau_1)\)
- 기존의 수식에서 달라진 점은 reward(=feature) mapping function 뿐이다.
- 해당 수식이 의미하는 바는, attribute \(\alpha_{i}\)를 기준으로 궤적 1이 더 적합한 경우에 대한 수식.
- Loss objective: Relative Attribute Strength Network(model) \(\begin{equation*} \mathcal{L}(\hat{\zeta}^{\boldsymbol{\alpha}}_{\theta}) = -\sum_{(\tau_{1},\tau_{2},y_{\text{attr}})\in D_p} \sum_{i=1}^{k} y_{i}(1)\log P^{\alpha_{i}}[\tau_{1} \succ \tau_{2}] + y_{i}(2)\log P^{\alpha_{i}}[\tau_{2} \succ \tau_{1}] \end{equation*}\)
- 저자도 언급하길, 이거는 단순히 Bradley-Terry objective에서의 Mapping 함수를 바꿔준 정도라고만 함.
- Introduction에서 언급한 single-step에 대해서만 추정하는 한계점을 \(\zeta\) 라는 mapping 함수를 통해 variable-length trajectory input에 대해서 적용할 수 있다는 점을 언급함.
- 이를 Transformer 구조로 학습하며, learnable embedding을 추가해 relative strength vector \(\boldsymbol{v^{\alpha}}\)를 학습하는 것을 목표로 함. (입력은 state-only 궤적을 받음.)
- Transformer를 거친 후에, 마지막 layer에는 linear layer를 통해 \(\boldsymbol{v^{\alpha}}\)를 얻음.
- 이를 Transformer 구조로 학습하며, learnable embedding을 추가해 relative strength vector \(\boldsymbol{v^{\alpha}}\)를 학습하는 것을 목표로 함. (입력은 state-only 궤적을 받음.)
- 학습이 수행된 이후에는 \(\hat{\zeta}^{\boldsymbol{\alpha}}_{\theta,i}(\cdot)\)을 통해 annotated dataset \(D_{G}=\{(\tau^{H},\boldsymbol{v^{\alpha}})\}\)을 얻음.
- 주의할 점은, 여기서 저장되는 trajectory는 모두 고정된 length \(H\)를 가짐. 위 데이터셋 \(D_{G}\)을 통해 diffusion training이 이루어짐. Attribute-Conditioning을 위해 수행한 과정.
- 저자는 Bradley-Terry objective를 수정하여 제시함.
-
Diffusion Training
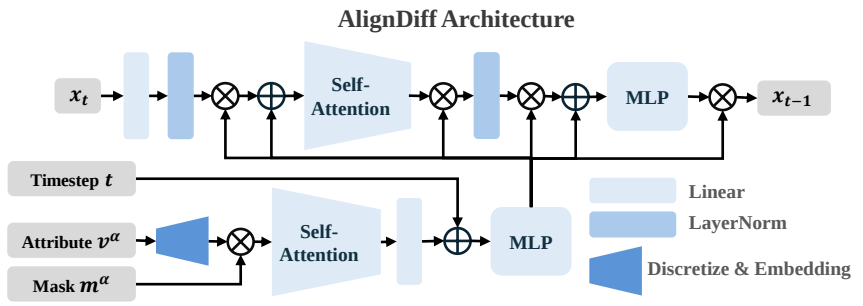 - DDIM 구조에 condition으로 \(\boldsymbol{v^{\alpha}},\boldsymbol{m^{\alpha}}\)을 줌. - [Conditioned / Unconditioned] noise predictor \([\epsilon_{\phi}(\boldsymbol{x}_{t},\boldsymbol{v^{\alpha}},\boldsymbol{m^{\alpha}})\) / \(\epsilon_{\phi}(\boldsymbol{x}_{t})]\) - masking \(\boldsymbol{m^{\alpha}}\)가 conditioning을 관여하므로, 한 개의 network를 학습하면 된다. - Diffusion backbone으로는 U-Net 대신에 DiT 모델을 사용하였으며, 구조에는 일부 수정이 있음. - Scalable Diffusion Models with Transformers (DiT) - Transformer-based Backbone.
- DDIM 구조에 condition으로 \(\boldsymbol{v^{\alpha}},\boldsymbol{m^{\alpha}}\)을 줌. - [Conditioned / Unconditioned] noise predictor \([\epsilon_{\phi}(\boldsymbol{x}_{t},\boldsymbol{v^{\alpha}},\boldsymbol{m^{\alpha}})\) / \(\epsilon_{\phi}(\boldsymbol{x}_{t})]\) - masking \(\boldsymbol{m^{\alpha}}\)가 conditioning을 관여하므로, 한 개의 network를 학습하면 된다. - Diffusion backbone으로는 U-Net 대신에 DiT 모델을 사용하였으며, 구조에는 일부 수정이 있음. - Scalable Diffusion Models with Transformers (DiT) - Transformer-based Backbone.-
이러한 condition을 잘 활용하기 위해 2개의 requirement가 있다고 함. 1. \(\boldsymbol{m^{\alpha}}\) should eliminate the influence of nonrequested attributes on the model while preserving the effect of the interested attributes _ masking vector를 통해 attribute 별로 독립적으로 고려할 수 있게 하겠다의 의미? 2. \(\boldsymbol{v^{\alpha}}\) cannot be simply multiplied with \(\boldsymbol{m^{\alpha}}\) and fed into the network, as a value of \(0\) in \(\boldsymbol{v^{\alpha}}\) still carries specific meanings. _ 1의 속성으로 인해 masking vector와 단순 곱을 사용하게 되면 잘못된 의미가 된다? 3. 이를 만족하기 위해 attribute-oriented encoder를 제안함. * \(\boldsymbol{v^{\alpha}}\)를 \(V\)개의 selectable token으로 표현해주기 위함.
\[v^{\alpha_{i}}_{d}=[\text{clip}(v^{\alpha_{i}},0,1-\delta)~\cdot~V]+(i-1)V,~i=i,\cdots,k\]- $$\delta$$: small slack variable. - This ensures that each of the V possible cases for each attribute is assigned a unique token. - 그렇게 임베딩을 거친 $$\boldsymbol{v^{\alpha}}$$는 both attribute category and strength의 정보를 포함하게 된다. - Loss objective: **Noise predictor loss of Diffusion mode** $$ \begin{equation*} \mathcal{L}(\phi) = \mathop{\mathbb{E}}_{(\boldsymbol{x}_{0},\boldsymbol{v}^{\alpha})\sim\mathcal{D}_{G},~t\sim\text{Uniform}(T),~\epsilon\sim\mathcal{N}(0,I),~\boldsymbol{m}^{\alpha}\sim\mathcal{B}(k,p)} \left\| \epsilon - \epsilon_{\phi}(\boldsymbol{x}_{t}, t, \boldsymbol{v}^{\alpha}, \boldsymbol{m}^{\alpha}) \right\|_{2}^{2} \end{equation*} $$
-
- AlginDiff Inference
- 앞선 과정에서 구한 attribute strength model \(\hat{\zeta}^{\boldsymbol{\alpha}}_{\theta}\)와 noise predictor \(\epsilon_{\phi}\)를 통해 AlginDiff를 소개한다. 저자는 DDIM 모델을 사용했으며, Inpainting 방식처럼 \(\kappa\)를 length \(S\) 내에서 반복적으로 candidate trajectory를 생성했다. \(\begin{equation*} \boldsymbol{x}_{\kappa_{i-1}} = \sqrt{\xi_{\kappa_{i-1}}} \left( \frac{\boldsymbol{x}_{\kappa_{i}} - \sqrt{1 - \xi_{\kappa_{i}}} \tilde{\epsilon}_{\phi}(\boldsymbol{x}_{\kappa_{i}})}{\sqrt{\xi_{\kappa_{i}}}} \right) + \sqrt{1 - \xi_{\kappa_{i-1}} - \sigma^{2}}_{\kappa_{i-1}} \tilde{\epsilon}_{\phi}(\boldsymbol{x}_{\kappa_{i}}) + \sigma_{\kappa_{i}} \epsilon_{\kappa_{i}} \end{equation*}\)
그렇게 최종 objective equation은 아래와 같다.
\[\mathcal{J}(\tau)=||(\boldsymbol{v^{\alpha}}-\hat\zeta^{\alpha}_{\theta}(\tau))\circ\boldsymbol{m^{\alpha}}||^{2}_{2}\]Each \(\tau\) in the candidate trajectories satisfies human preference \((\boldsymbol{v^{\alpha}},\boldsymbol{m^{\alpha}})\) a priori. Then we utilize \(\hat{\zeta}^{\alpha}_{\theta}\) to criticize and select the most aligned one to maximize the following objective:
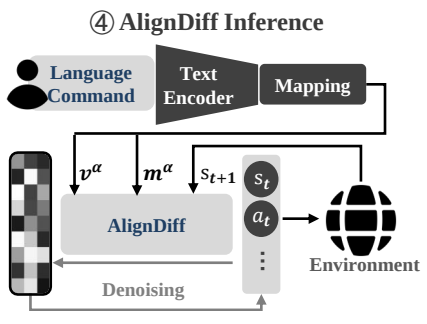
Inference Flowchart.
실제 Inference가 수행될 때에는 language command가 주어지고, 이를 Sentence-BERT에 태워서 corpus와 mapping을 거치게 된다. → 의도한 attribute와 가장 유사한 것으로 mapping 됨.
Experiments
아래의 4개의 질문에 대한 답을 하기 위해 실험을 설계함.
- Matching (RQ1): Can AlignDiff better align with human preferences compared to other baselines?
- Switching (RQ2): Can AlignDiff quickly and accurately switch between different behaviors?
- Covering (RQ3): Can AlignDiff cover diverse behavioral distributions in the dataset?
- Robustness (RQ4): Can AlignDiff exhibit robustness to noisy datasets and limited feedback?
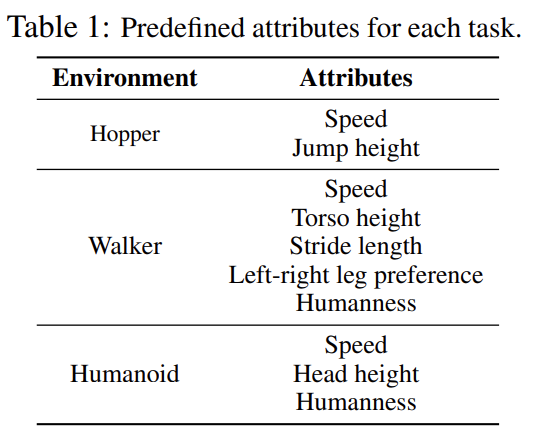
실험에서 사용된 Attribute.
- Baselines
- Goal-conditioned behavior clone (GC): RvS (RL VIA SUPERVISED LEARNING)
- RvS: What is essential for offline RL via supervised learning? (ICLR, 2022)
- conditioning on reward or goal / Simple 2-Layered MLP architecture
- RvS: What is essential for offline RL via supervised learning? (ICLR, 2022)
- Sequence modeling (SM): Decision Transformer (DT)
- TD Learning (TDL): TD3BC
- A minimalist approach to offline reinforcement learning. (NeurIPS, 2021)
- TD3 policy update eqn.에 behavior cloning regularization term을 추가함.
- dataset의 state feature에 대해 normalize를 수행함.
- 저자가 소개하길, 이는 RBA의 upgrade 버전이라고 함.
- A minimalist approach to offline reinforcement learning. (NeurIPS, 2021)
- Goal-conditioned behavior clone (GC): RvS (RL VIA SUPERVISED LEARNING)
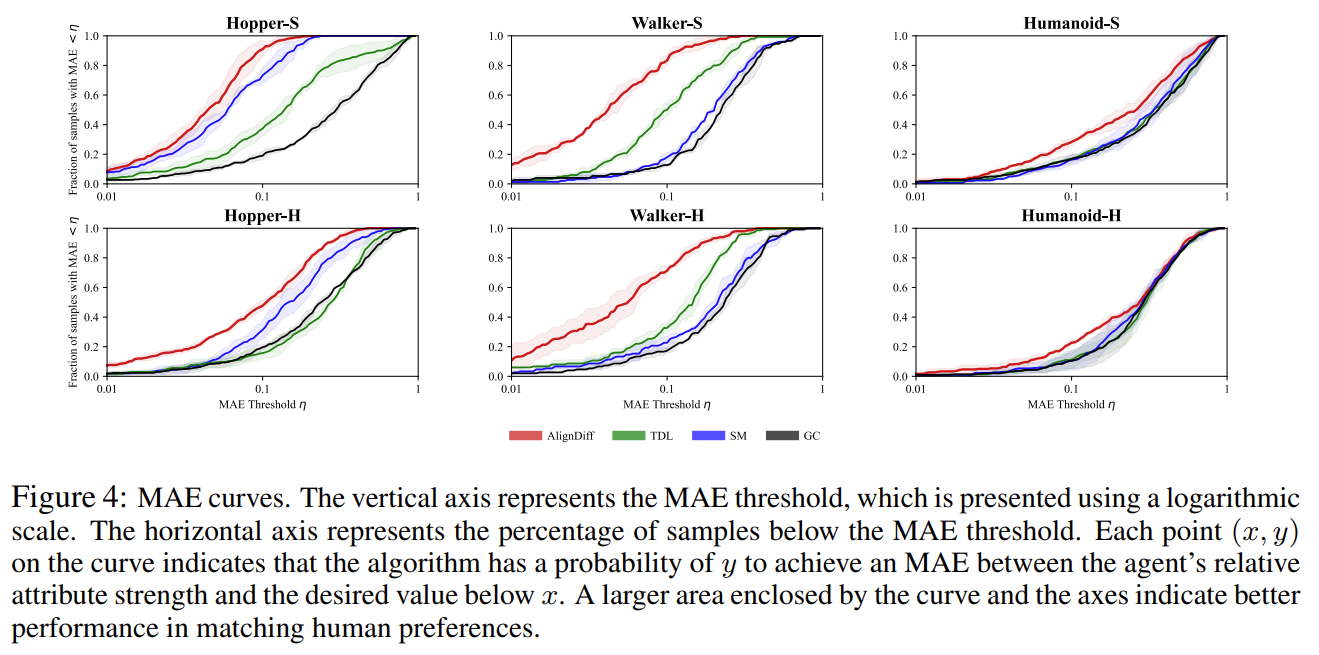
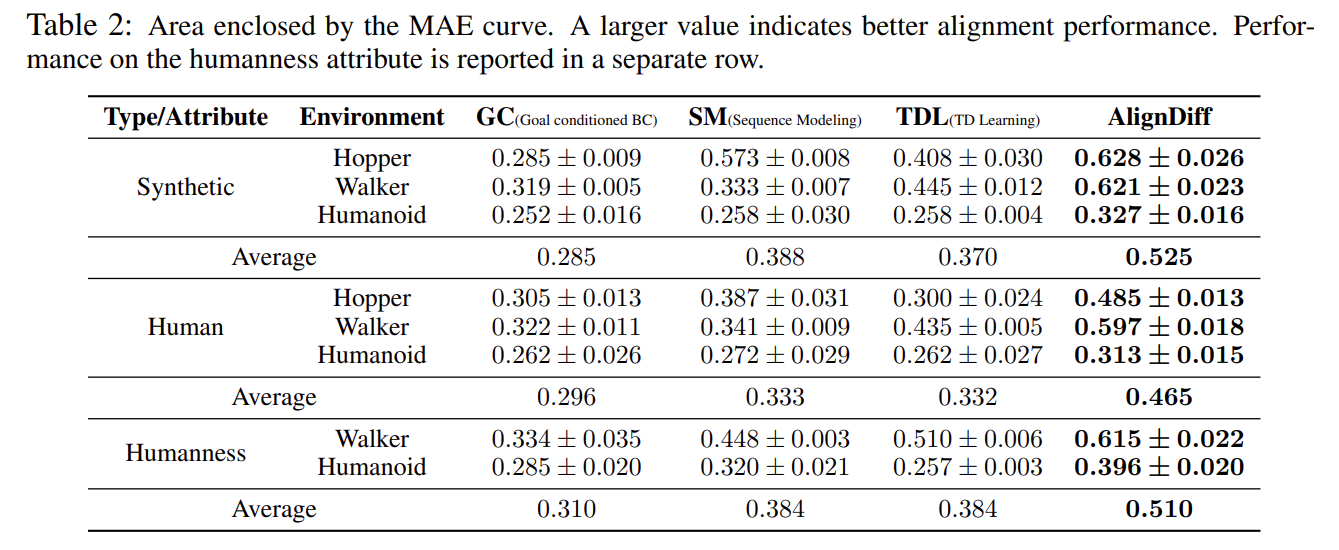
-
Evaluation by attribute strength model:
- The mean absolute error(MAE) between the evaluated and target relative strength를 metric으로 삼음.
-
Track the changing target attributes:
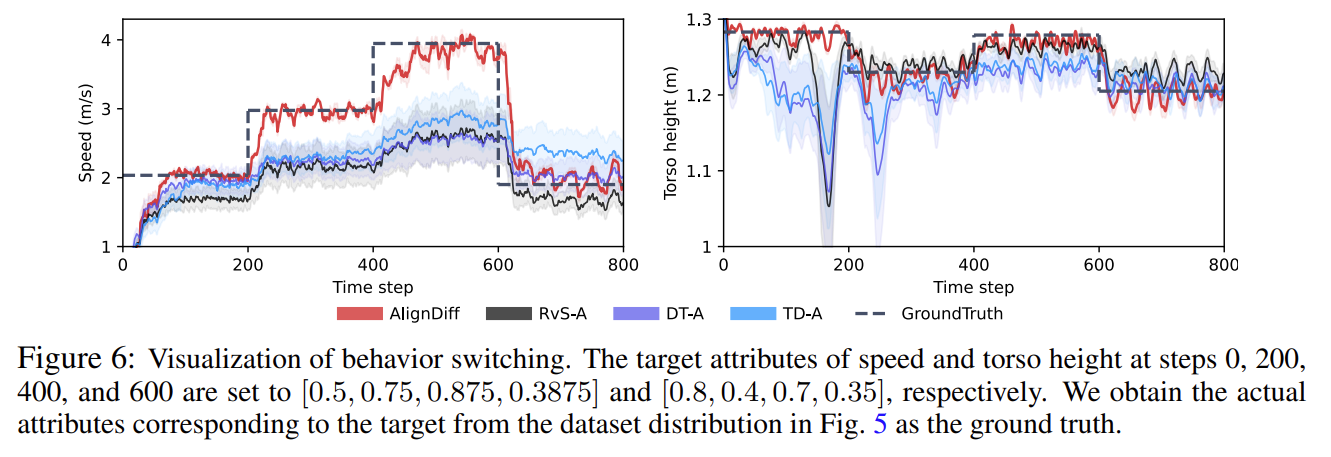
- 총 800번의 simulation step 중, target attribute \(\boldsymbol{v^{\alpha}}_{\text{targ}}\)을 \((0,200,400,600)\)에서 수정을 함. - 빠르게 tracking 한다는 결과를 보여줌.
-
Covering attribute strength distribution:
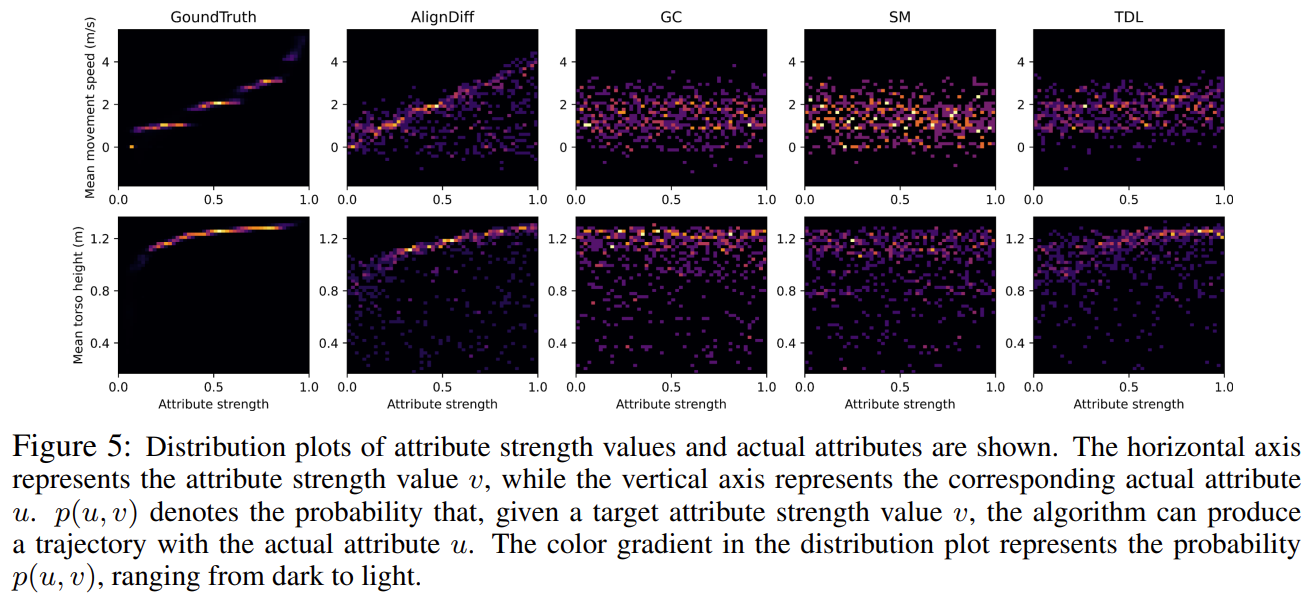
- AlignDiff 을 통해 얻은 network \(\hat\zeta^{\alpha}_{\theta}(\tau)\)가 GT와 유사하게 값을 잘 추정해낸다는 것을 보여줌.
Conclusion
- Abstractness
- RLHF로 Human preference에 대한 dataset을 통해 preference를 quantify.
- Mutability
- 변화하는 preference를 conditioned-diffusion model로 해결함.
Appendix
- Implementation details.
- Dataset details.
Thoughts
- Abstractness와 Mutability라는 용어를 처음으로 제시했으며, 각각에 해당하는 한계점을 잘 녹여냈음.
- Abstractness를 위해 RLHF labeling을 거치며, appendix에서 이 data에 대한 reliableness도 보장하였음.
- Attribute 요소를 포괄하는 상위 개념의 Persona?로 정의해서 표현해보는 방향도 재밌을 것 같다. (교수님 취향)
- Mutability라는 용어로 preference의 변화를 표현했으며, 실험 결과도 이를 잘 보여주었음. 다만 Figure 6.에서 보듯이, oscilation 이 꽤 심하게 있는 것 같음.
- 해당 용어는 Time-varying 뿐만 아니라, 사용자에 따라 달라지는 preference도 포함한 개념.
- Agent 끼리의 Attribute를 transfer 해주는 것도 고려하면 재밌을 것 같음.
- Figure 5.를 통해 동일한 attribute 내에서는 interpolation이 가능하다고 표현했으며 잘 보여줌.
- 동일 Agent 혹은 서로 다른 Agent의 서로 다른 Attribute 간의 interpolation도 가능하면 매우 파격적일 것 같음.
- ex) skill composition or preference composition 느낌으로?
- 동일 Agent 혹은 서로 다른 Agent의 서로 다른 Attribute 간의 interpolation도 가능하면 매우 파격적일 것 같음.
- Diffusion model을 사용하다보니 Inference에 시간이 오래 걸린다고 한다. 구체적인 inference 시간도 같이 알려줬으면 좋았을 것 같다. (Baseline과 비교하여)
- Abstractness를 위해 RLHF labeling을 거치며, appendix에서 이 data에 대한 reliableness도 보장하였음.
- Dataset
- 실험에서 사용한 Attribute가 조금 단순하다고 여겨짐. 다만, 논문의 예시들은 시각적으로 효과적인 차이를 잘 보여준 것 같음. 이러한 Attribute를 더 다양하고 적은 label 데이터로 수행할 수 있으면 좋을 것 같음. (혹은 자동 labelling)
Reference papers
- Aligning artificial intelligence with human values: reflections from a phenomenological perspective (SpringerLink, 2021)
- 한 문장 요약:
This paper contributes the unique knowledge of phenomenological theories to the discourse on AI alignment with human values.
- 서술적인 내용들로만 이루어져 있음.
- 한 문장 요약:
- Relative behavioral attributes: Filling the gap between symbolic goal specification and reward learning from human preferences. (ICLR, 2023)
- 한 문장 요약:
In most cases, humans are aware of how the agent should change its behavior along meaningful axes to fulfill their underlying purpose, even if they are not able to fully specify task objectives symbolically: allows the users to tweak the agent behavior through symbolic concepts.
- Attribute를 표현한 논문
- 한 문장 요약:
- Inverse Reward Design (읽어볼 것 / NIPS, 2017)
- 한 문장 요약:
We introduce inverse reward design (IRD) as the problem of inferring the true objective based on the designed reward and the training MDP. We introduce approximate methods for solving IRD problems, and use their solution to plan risk-averse behavior in test MDPs.
- 한 문장 요약:
- Leveraging Approximate Symbolic Models for Reinforcement Learning via Skill Diversity (PMLR, 2022)
- 한 문장 요약:
Symbolic model과 MDP를 합쳐서 skill learning을 수행해보자. (Approximate Symbolic-Model Guided Reinforcement Learning)
- 한 문장 요약:
- Imitating Human Behaviour with Diffusion Models (2023, ICLR)
- 한 문장 요약:
We then propose that diffusion models are an excellent fit for imitating human behavior. (This paper studies their application as observation-to-action models for imitating human behavior in sequential environments.) - Diffusion + KDE 방법론: Diffusion 모델로 여러 샘플을 얻고, 그에 해당하는 KDE 구조를 사용함.
- observation-to-action diffusion models 을 분석하고 소개함.
-
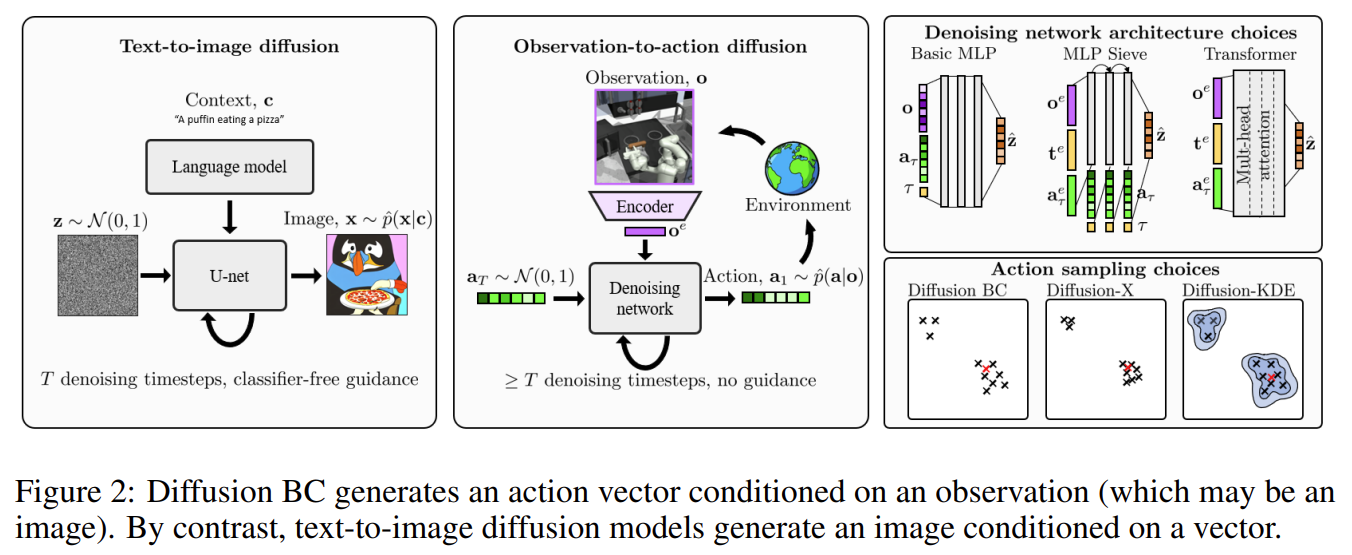
‘Diffusion-X’ and ‘Diffusion-KDE’ as variants of Diffusion BC, that mirror this screening process by encouraging higher-likelihood actions during sampling. For both methods, the training procedure is unchanged (only the conditional version of the model is required)
- 한 문장 요약:
Enjoy Reading This Article?
Here are some more articles you might like to read next: