[paper-review] Relative Behavioral Attributes: Filling the Gap between Symbolic Goal Specification and Reward Learning from Human Preferences
ICLR 2023. [Paper] [Project Page] [Github]
Lin Guan, Karthik Valmeekam, Subbarao Kambhampati School of Computing & AI Arizona State University Tempe, AZ 85281, USA
27 Feb 2023
한 문장 요약
요약: tacit behavior를 attribute라고 정의하고, trajectory 내에서 relative behavior attribute를 추정하자. 즉, Relative Behavioral Attributes(RBA)를 정의해, symbolic feedback으로부터 희망하는 agent behavior를 얻자.
In most cases, humans are aware of how the agent should change its behavior along meaningful axes to fulfill their underlying purpose, even if they are not able to fully specify task objectives symbolically: allows the users to tweak the agent behavior through symbolic concepts.
Keyword: Relative Behavioral Attributes
Introduction
- Agent의 Behavior를 정의하는 방식은 크게 2가지가 있다.
- Reward function을 직접 지정해주는 경우.
- 직접 특정 behavior를 유도하게끔 하는 수식적인 reward function을 explicit하게 정하는 것이며, 논문에서는 이를
symbolic reward machine이라고 표현함. - 하지만 exact description이 가능한 경우는 매우 한정적이며(=
domain specific),expert knowledge를 요한다.
- 직접 특정 behavior를 유도하게끔 하는 수식적인 reward function을 explicit하게 정하는 것이며, 논문에서는 이를
- 궤적으로부터 Reward function을 추정하는 경우.
- 기존의 PBL은 궤적에 대해 이러한 feedback(=binary comparison) 과정을 거쳐 reward function을 추정해왔으며, 이는 preference labelling에 대한 cost가 높았다.
- 그리고 학습된 neural network는 typically inscrutable 하므로 실질적으로 reward model을 재사용할 수도 없으며, internal representation을 해석할 수도 없다.
- Reward function을 직접 지정해주는 경우.
- 위 두 방식에서 수행된 behavior에 대한 표현력은 제한적이었으며, 이러한 한계점을 해결하기 위해 저자는
attribute를 정의하며 논문을 시작한다.- 기존의 pbl에서 사용되던
feature function\(\phi (\xi)\) 와 유사하게,attribute라는 용어를 정의하며, 이는 behavior에 대해 symbolic concept을 가진다. (e.g., increasing the softness or speed of agents’ movement) - 기존에 computer vision에서도
attribute라는 용어가 사용되어왔지만, 이는 single image에서만 활용됐으며, agent의 궤적에 활용하는 것은 본 논문이 첫 시도임.
- 기존의 pbl에서 사용되던
Preliminaries
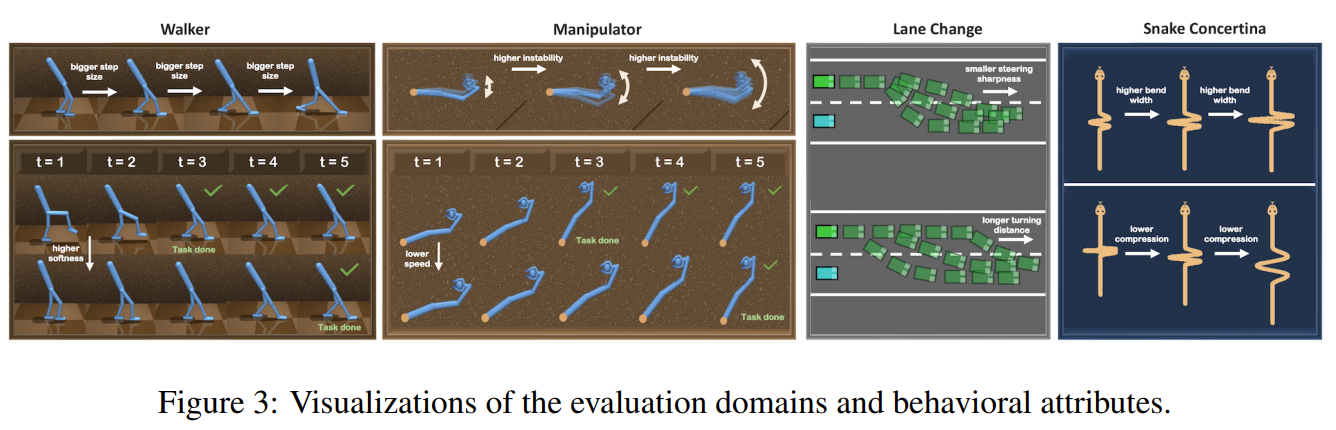
Fig. 1: Visualization of Behavior Attributes.
- Attribute: agent’s behavior features(=descriptions)
- 총 4개의 Task에 대해서 9개의 Attribute를 정의했음.
Appendix A.1참조.
- 총 4개의 Task에 대해서 9개의 Attribute를 정의했음.
- \(\alpha \in \mathcal{A}\): attribute의 종류,
e.g., softness of movement, step(=stride) size - \(h\):
attribute를 binary masking 해주는 역할. - \(v^{ {\alpha}_{i} }_{t}\): target attribute-score vector, \(\alpha_i\)에 해당하는 target scalar value
- \(\mathcal{D}\): State-only Trajectory pool
- \(\zeta_{\sigma}(\tau ', \alpha_{i}) \simeq \boldsymbol{v}^{\alpha_{i}}_{t}\): target attribute score \(\boldsymbol{v}\)에 대한 mapping function \(\zeta\)
Methodology
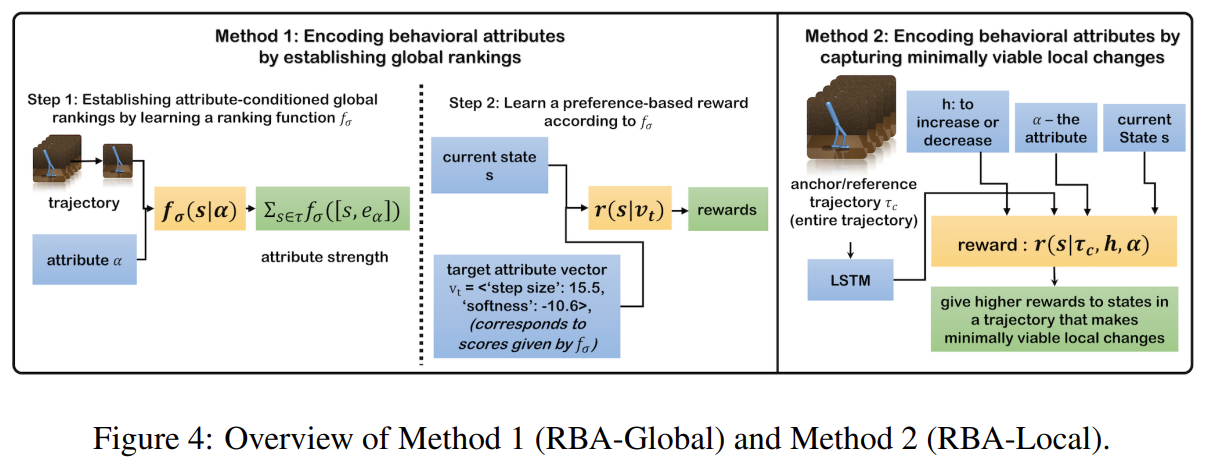
Fig. 2: Overall framework of RBA.
Our goal is to construct a reward function that allows end users to iteratively adjust attribute strengths presented in the agent’s behavior.
Section 4.1 Personalizing Agent Behavior Via Relative Behavior Attributes
- Trajectory sequence에서 relative strength of some property(=
attribute)를 찾으려는 것이 목적이며, 이를 2개의 phase로 구분한다.- Leraning an attribute parameterized reward function (no interaction with the end user).
To learn a reward function that internally learns a family of rewards that correspond to behaviors with diverse attribute strength
- given a subset of labelled trajectories from an offline behavior dataset \(\mathcal{D}\).
- 여기서 Training label은 expert engineer 혹은 developer가 제공하는 것으로 한정한다.
- given a subset of labelled trajectories from an offline behavior dataset \(\mathcal{D}\).
- Interaction with the end user (Supporting end users in the loop).
Once an attribute parameterized reward function is learned, any incoming users can leverage it to personalize the agent behavior through multiple rounds of query
- set of attribute pairs \(\{ (\alpha, h)\}\) 를 기준으로 user가 feedback을 준다.
whether the current behavior is desirable.
- Attribute representation은 2개로 정의했으며, 1) Index of \(\alpha\), 2) a Natural-Language Description of \(\alpha\).
- set of attribute pairs \(\{ (\alpha, h)\}\) 를 기준으로 user가 feedback을 준다.
- Leraning an attribute parameterized reward function (no interaction with the end user).
- 저자는 총 2개의 method 를 제시함. (1) RBA-Global / (2) RBA-Local
Section 4.2 Modeling Behavior Attributes by Establishing Global Rankings: RBA-Global
-
RBA-Global은 2개의 과정으로 이루어진다.
-
Learn attribute strength estimator \(\zeta_{\sigma}\)
- 기존의 Bradley-Terry model에서 exponential term이 zeta 함수로 변경되었으며, 궤적과 attribute가 주어졌을 때 그에 상응하는 strength 값으로 attribute mapping function zeta를 학습해주는 과정임.
- 즉, attribute에 대한 ranking을 학습하는 과정임.
establishing a global ranking among all possible behaviors according to any given attribute \(\alpha\). Orderings according to different attributes \(\{ (\tau^{0} \succ \tau^{1} \succ \cdots \tau^{N} | \alpha)\}\) or a set of ranked trajectory pairs \(\mathcal{D}_{l}=\{(\tau^{i} \succ \tau^{j} | \alpha)\}\)
- 저자는 modified state-only version of Bradley-Terry model을 제안한다.:
Rather than assuming that the ranking is governed by the latent user preferences, We assume the ranking is determined by the given attribute \(\alpha\):
- where \(f_{\sigma}\) is an attribute conditioned ranking function with parameters \(\sigma\), \([\cdot, \cdot]\) is the vector concatenation operation, and \(e_{\alpha}\) is the embedding of attribute \(\alpha\).
- \(e_{\alpha}\) can either be a one-hot vector or a sentence embedding generated by any pretrained natural language sentence encoder like \(\text{Sentence-BERT}\).
-
Learn dense reward function $$r_{\theta}(s v_t= \left< v^{\alpha_{1}}{t}, \cdots, v^{\alpha{k}}_{t} \right>)$$ - trajectory pool에서 3개의 궤적 \(\tau_0, \tau_1, \tau_2\)을 sample하고, \(\tau_0\).을 target behavior로 간주하여 나머지 두 궤적 중 어떠한 것이 더 적합한지 cumulative reward를 통해 판단하게 되며, reward function을 학습하게 된다.
- 위 과정에서는 human labelling 과정이 필요없다. zeta function이 자동으로 attribute labelling을 수행해주기 때문에.
-
Section 4.3 Modeling Behavior Attributes by Capturing Minimally Viable Local Changes: RBA-Local
- RBA-Global에 대해서 확장된 개념이며, 보다 많은 수의 attribute가 있을 때에 효율적으로 학습하기 위해 본 방법론으로 확장했다고 주장한다.
- 여기서는 \(\zeta\) function을 학습하지 않고, 곧바로 reward function \(r\) 을 학습한다.
Our goal is to construct a reward function that gives higher cumulative rewards to trajectories that have some minimal but noticeable change in \(\alpha\) in the direction specified by \(h\) while keeping other unmentioned attributes unchanged. We refer to such minimal but noticeable changes as minimally viable local changes, and the queried trajectory \(\tau_{c}\) as the anchor trajectory.
-
$$r_{\theta}(\cdot \alpha, h, \tau_{c})\(를 학습하는 것이며, 이는 minimal but noticeable change in\)\alpha$$ 를 포착하는 것이 목적이다. - 여기서 Dataset에서 가져오는 trajectory pair의 구조도 조금 달라진다; \(\mathcal{D}_{l}=\{ (\tau_{c}, \tau_{t}, \alpha, h)\}\)
- \(\tau_{c}\): anchor trajectory
- \(\tau_{t}\): a trajectory that reflects some minimally viable local changes to the anchor trajectory \(\tau_{c}\)
-
이에 대해 queried trajectory \(\tau_{c}\) 를 anchor trajectory로 정의하며, 해당 궤적의 attribute \(\alpha\)를 기준으로 negative sample과 비교하여 trajectory \(\tau_{t}\)와 PBL을 수행해주는 과정이다.
\[\begin{equation*} \mathrm{P}_{\sigma}[\tau^{t} \succ \tau^{n} | \alpha, h, \tau_{c}] = \frac{\exp \sum_{s \in \tau_{t}} r_{\theta}([s, e_{\alpha}, h, \phi(\tau_{c})])}{\exp \sum_{s \in \tau_{n}} r_{\theta}([s, e_{\alpha}, h, \phi(\tau_{c})] ) + \exp \sum_{s \in \tau_{t}} r_{\theta}([s, e_{\alpha}, h, \phi(\tau_{c})] )} \end{equation*}\]- where \(\tau_{n}\) is a negative sample, \([\cdot]\) is the vector concatenation operation, and \(\phi(\tau_{c})\) is a sequence encoder that encodes the anchor trajectory \(\tau_{c}\) to a compact latent representation. Note that \(\phi(\cdot)\) is a sub-module of \(r_{\theta}\) and it’s jointly optimized with \(r_{\theta}\).
-
\(e_{\alpha}\) can either be a one-hot vector or a sentence embedding generated by any pretrained natural language sentence encoder like \(\text{Sentence-BERT}\).
- 저자는 이러한 구조가 Prompt-DT 논문과 유사하다고 밝히며, 저자가 주장하는 차이점은 다음과 같다.
- RBA method는 단순히 prompt의 behavior를 모방하는 것에 그치지 않고, prompt 내용(=
attribute)을 수정하는 것을 학습한다고 한다.
- RBA method는 단순히 prompt의 behavior를 모방하는 것에 그치지 않고, prompt 내용(=
- 저자는 이러한 구조가 Prompt-DT 논문과 유사하다고 밝히며, 저자가 주장하는 차이점은 다음과 같다.
- 다만 이 방법론은 특정 attribute의 local change를 고려하므로 search space가 복잡해지며, 아무런 궤적을 막 가져오면 안 되고 local change가 잘 반영된 궤적을 가져와야 한다는 단점이 있다.
Experiments
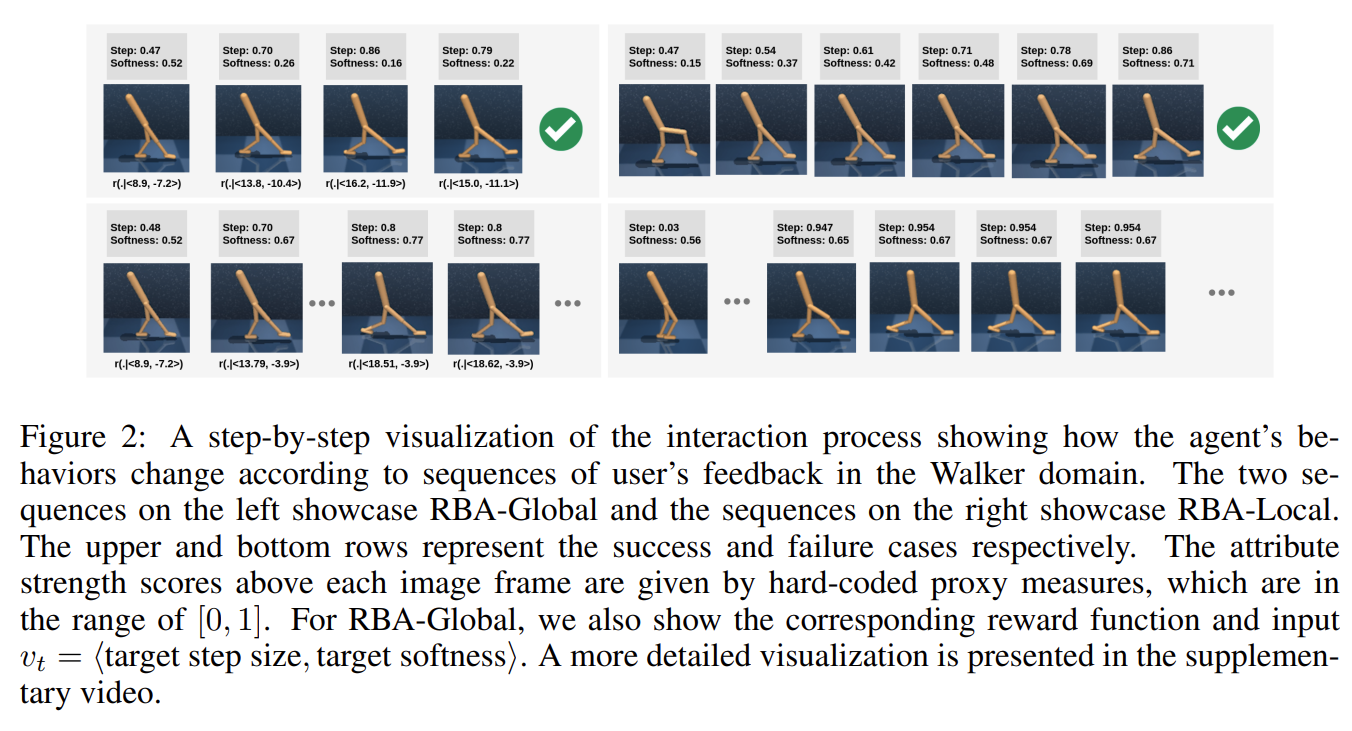
Fig. 3: Interaction Visualization
-
Baselines
- PbRL in (Christiano et al., 2017; Lee et al., 2021)
- PbRL
- PEBBLE
- PbRL in (Christiano et al., 2017; Lee et al., 2021)
-
Results on RBA-Global:
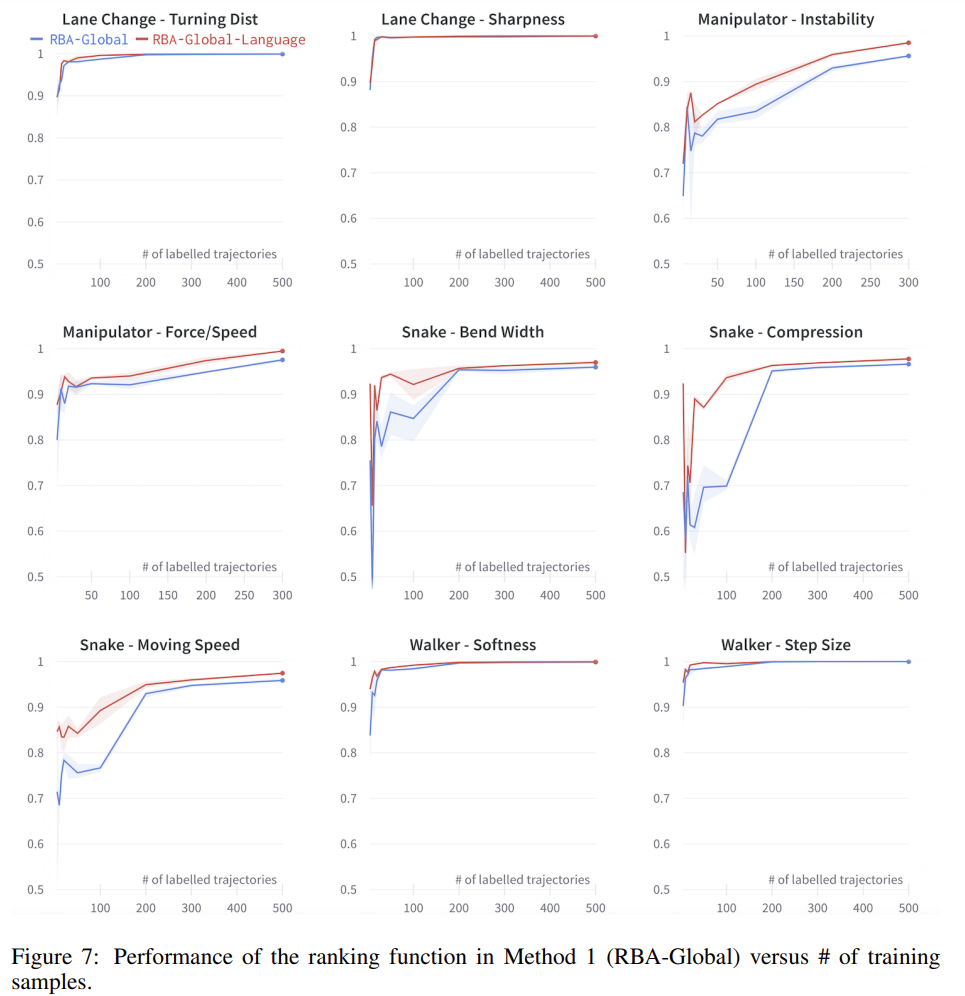
Fig. 4: Performance of RBA-Global
- Results on RBA-Local:
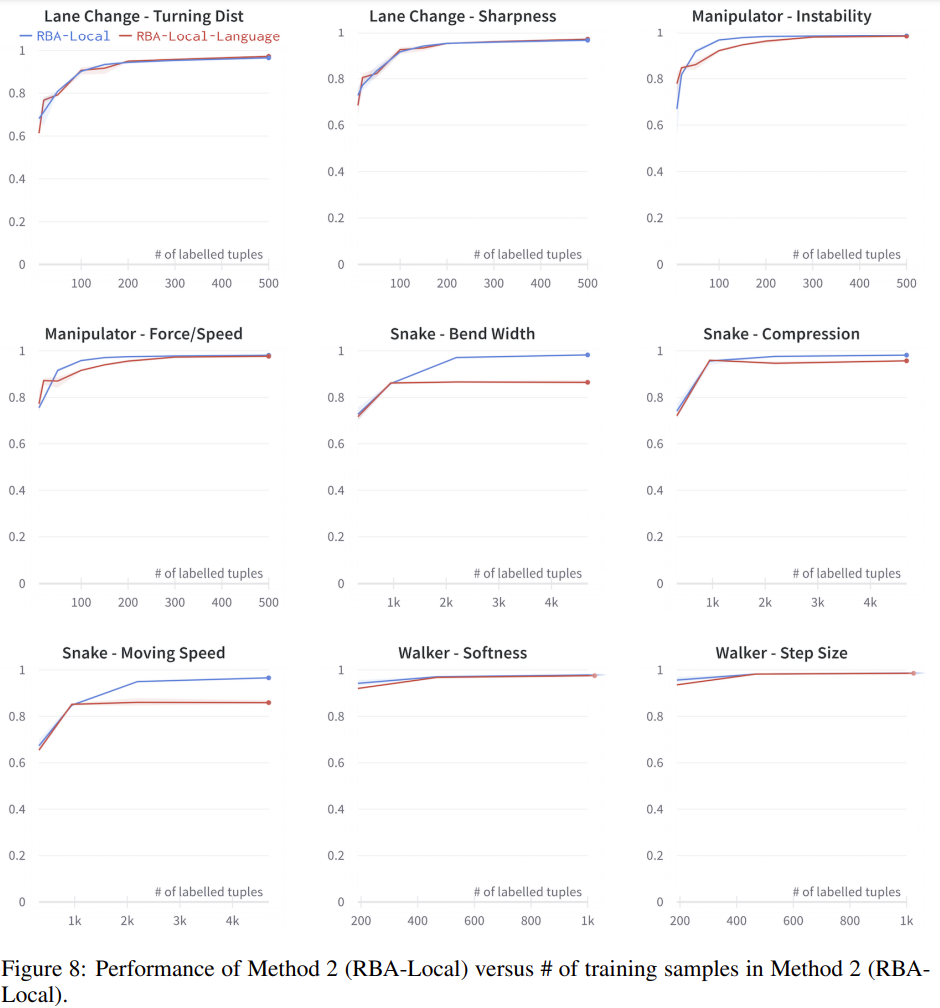
Fig. 5: Performance of RBA-Local
Appendix
- Behavior Attribute details.
- Implementation details.
- Experiment details.
Thoughts
- Behavior PBL을 처음으로 제시한 논문인 것 같습니다. 본 논문에서 언급한 것처럼,
attribute라고 정의해, 말로 설명하기 어려운tacit behavior에 대해서 수행하는 것이 가장 큰 contribution 입니다. 다만 실제 실험을 보았을 때에는tacit behavior라고 표현하지 않아도 될 요소를attribute로 삼아 연구를 수행한 것이 아쉬웠습니다. (e.g., moving speed, instability of the movement) - RBA-Global 방법론은 기존에 수행해오던 PBL과 크게 다른 점은 없어보였고, feature function을
attribute conditioned하게 해준 것에 차이가 있는 것 같습니다. 그에 반해 RBA-Local 방법론은 human labelling을 필요로하지 않아 제가 느끼기에는 덜 수고스럽다는 점에서 유요하다고 여겨집니다. (50~100개 정도의 궤적에 대해 interaction을 거치면 수렴하는 듯한 양상을 보입니다.) - 코드가 공개되어 있어서, 실제로 돌려보고 구체적으로 각각의 parameter가 어떻게 적용되는지 공부하려고 합니다.
Enjoy Reading This Article?
Here are some more articles you might like to read next: