[paper-review] Predicting Object Interactions with Behavior Primitives: An Application in Stowing Tasks

CoRL 2023 (Oral). [Paper] [Code]

Haonan Chen, Yilong Niu^*, Kaiwen Hong^*, Shuijing Liu, Yixuan Wang, Yunzhu Li, Katherine Driggs-Campbell

University of Illinois Urbana-Champaign

(* indicate equal contribution)

2023

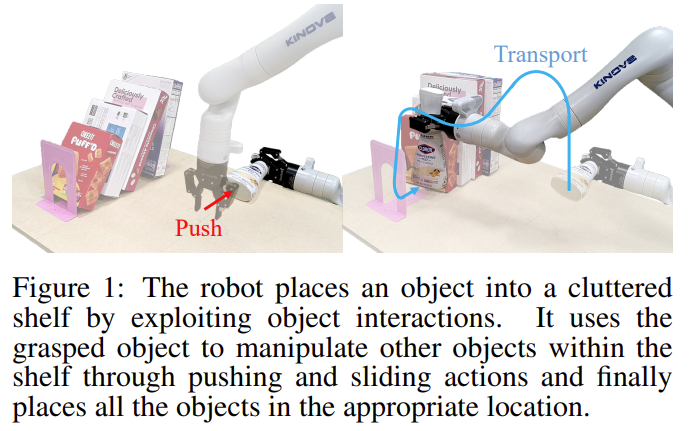
Fig. 1: Task description about Stowing.

한 문장 요약

요약: Stowing task에 대해서 one-shot demonstration으로 policy를 학습하자.

Stowing: defined as relocating an object from a table to a cluttered shelf.

We propose a framework that uses Graph Neural Networks (GNNs) to predict object interactions within the parameter space of behavior primitives.

Previous Research

Stowing task는 아래 세 개의 측면에서 어려움이 있었음.

Long-horizon nature: contact/friction에 대한 정의가 필요함.
Multi-object interaction: struggle with adaptability.
Variety of objects: need for expensive data collection and human labelling.

Contribution

minimal demonstration으로 학습할 수 있는 model-based imitation learning framework를 제시함.
Stowing benchmark를 제시함. (comprehensive long-horizon task)
저자가 제안한 모델에 대한 Effectiveness와 Generalization을 검증함.

Approach

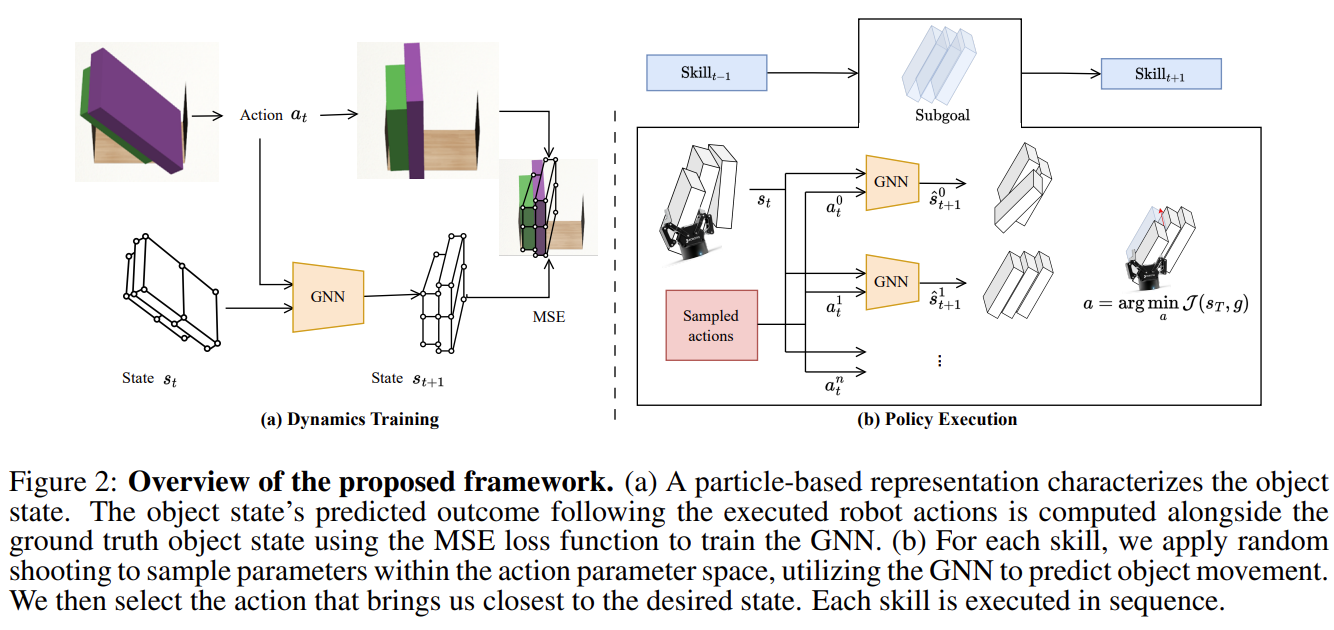
Fig. 2: Overview of STOW-GNN.

2개의 모듈로 나뉜다.

GNN predicts system dynamics.
A primitive-augmented trajectory optimization method achieves subgoals from a single demonstration.

Learning Forward Dynamics via GNN

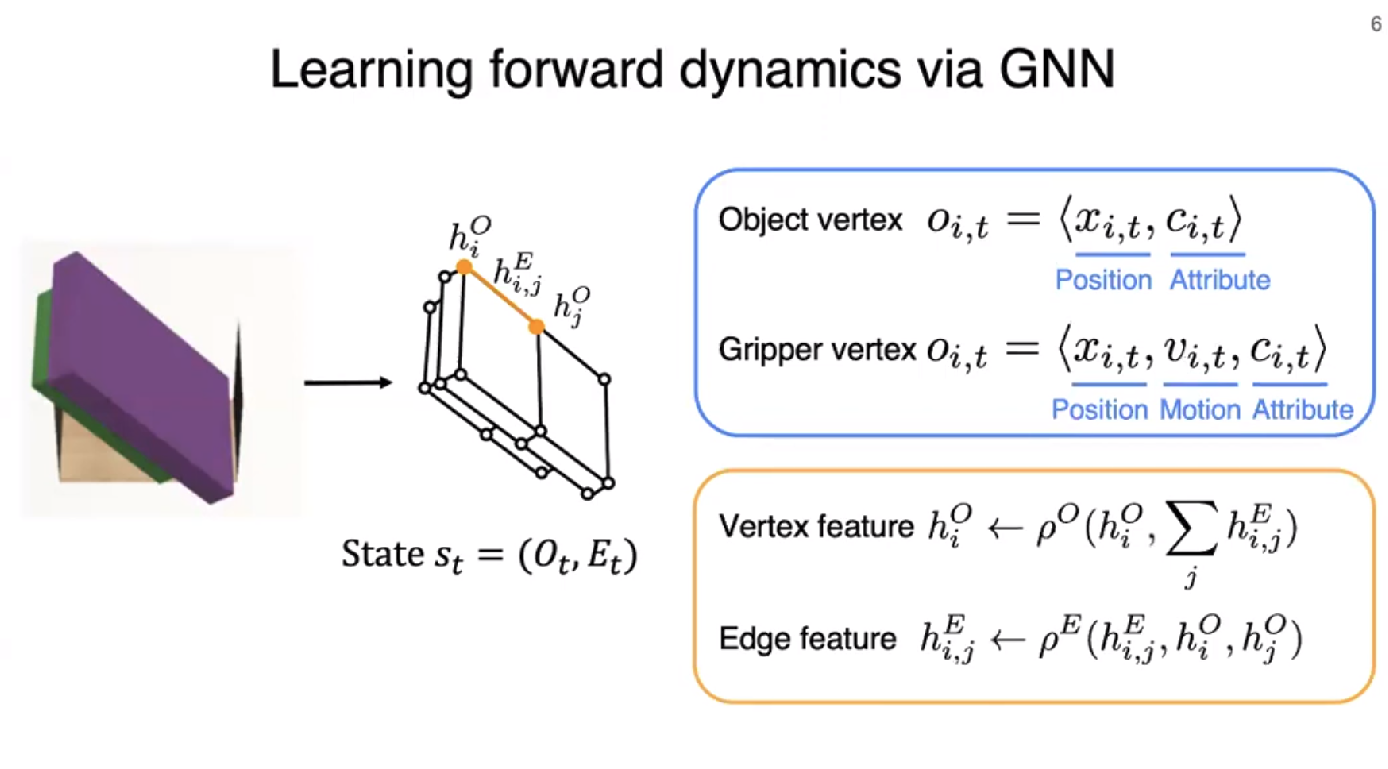
Fig. 3: Description about GNN Network.

Graph Construction (Terminology)
- Rigid-body system을 System state \(s \in \mathcal{S}\) with \(\mathcal{M}\) objects and \(\mathcal{N}\) particles 로 표현한다.
  - graph state \(s_{t}= \left(\mathcal{O}_{t}, \mathcal{E}_{t} \right)\)
  - grph’s vertices \(\mathcal{O}_{t}\): object’s particles.
    - \(o_{i,~t}=\left< x_{i,~t},~c_{i,~t} \right>\), particles’s position \(x_{i,~t}\) and object’s attributes \(c_{i,~t}\)
  - grph’s edges \(\mathcal{E}_{t}\): relations between particles. It is formed when the distance between two vertices is less than a specified threshold.
    - \(\mathcal{E}_{t}\): 2개의 경우로 relation을 정의한다.
      1. Intra-object relations: Between different particles within the same object or across different objects.
      2. Gripper-to-object relations: Between particles from the objects and the robot’s gripper.
        
        \(e_{k}=\left< i_k, j_k, c_k \right>\): \(i_k, j_k\) are reciever and sender particles, respectively. \(k\) is edge’s index, \(c\) is object’s attribute
- Action을 \(\mathcal{A}\)로 표현한다. 이는 \(\left< \text{skill type, associated parameter} \right>\) 를 포함하고 있다.
- \(\mathcal{T}\): (dynamic object 각각에 대해) \(\mathcal{M}\) 개의 rigid transformation을 의미한다.
- Dynamics function \(\Phi: \mathcal{S\times A \rightarrow T}\)
GNN을 사용하는 이유는 단순히 behavior primitive를 수행했을 때의 system’s state를 예측하기 위함이다.

그렇게 모든 vertices와 edges는 MLP를 거쳐 latent vertex \(h^{O}_{i}\), edge \(h^{E}_{i,j}\) representation을 아래의 수식으로 표현할 수 있게 된다.

\[\begin{equation} h^{E}_{i,j} \leftarrow \rho^{E} \left( h^{E}_{i,j}, h^{O}_{i}, h^{O}_{j} \right),~~~ h^{O}_{i} \leftarrow \rho^{O} \left( h^{O}_{i}, \sum_{j} h^{E}_{i,j} \right) \end{equation}\]

여기서 \(\rho^{E},~\rho^{O}\)는 각각 edge, vertex의 message passing function (i.e., MLP)을 의미한다.

그리고 각 물체의 rigid transformation는 decoder output의 mean으로 결정된다. (Fig. 2(b)를 참고하면 됨.)

그리고 마지막으로 control action은 아래와 같이 정의된다. (gripper’s planned position and motion defined by particles.)

\[o_{i,t} = \left< x_{i,t}, v_{i,t}, c_{i,t} \right>\]
- \(x_{i,t}\): current position of gripper
- \(v_{i,t}\): planned motion of the gripper

Control with the Learned Dynamics

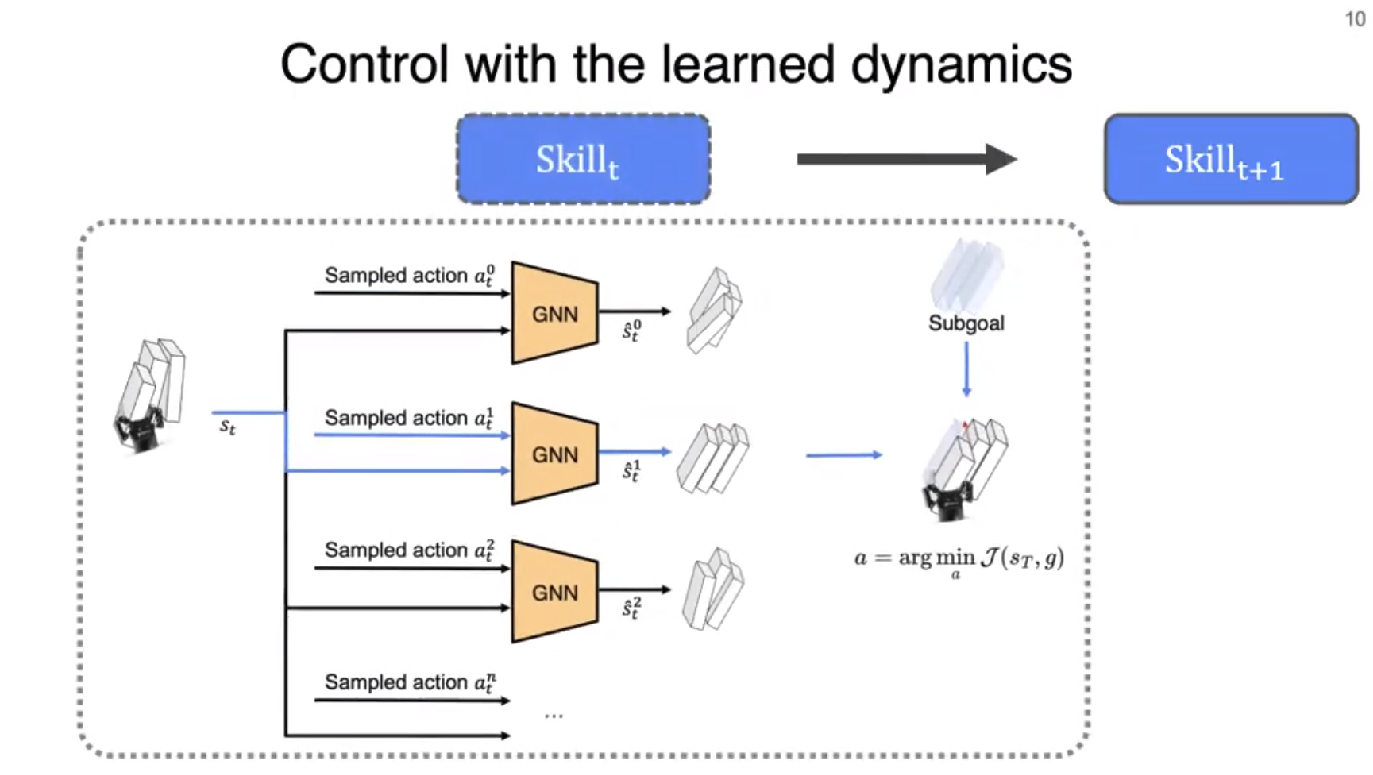
Fig. 4: Description about Skill selection.

Behavior primitive를 정의해 Operation Space Control로써 action이 수행된다. 저자는 총 3개의 Primitive를 정의한다.

Sweeping: \(y,h,d,\theta\)로 정의됨.
- \(y\): starting offset in the shelf direction
- \(h\): sweeping height
- \(d\): sliding distance
- \(\theta\): angle of gripper rotation
Pushing: \(x,y,d\)로 정의됨.
- \((x,y)\): starting push(nudge) position
- \(d\): distance of the push
Transporting: \(y,h,d,\theta\)로 정의되며, Sweeping과 동일함. 다른 점은, 물체를 쥐고 있다는 점이다.

아래의 Objective loss를 최소화하는 action \(a_{p}\)를 찾는 것이 목적이다.

\[\begin{equation} a_{p} = \arg \min_{a_{p}} \mathcal{J} (s_{T}, g) \end{equation}\]

\(a_{p}\): skill parameter
\(g\): Keyframes collected during demonstrations.

요약: \(\Phi\)로 Forward prediction을 통해서 rigid body system의 future state를 예측하고, lowest cost를 갖는 skill parameter \(a_{p}\)를 찾는 것이다.

Experiment Setup

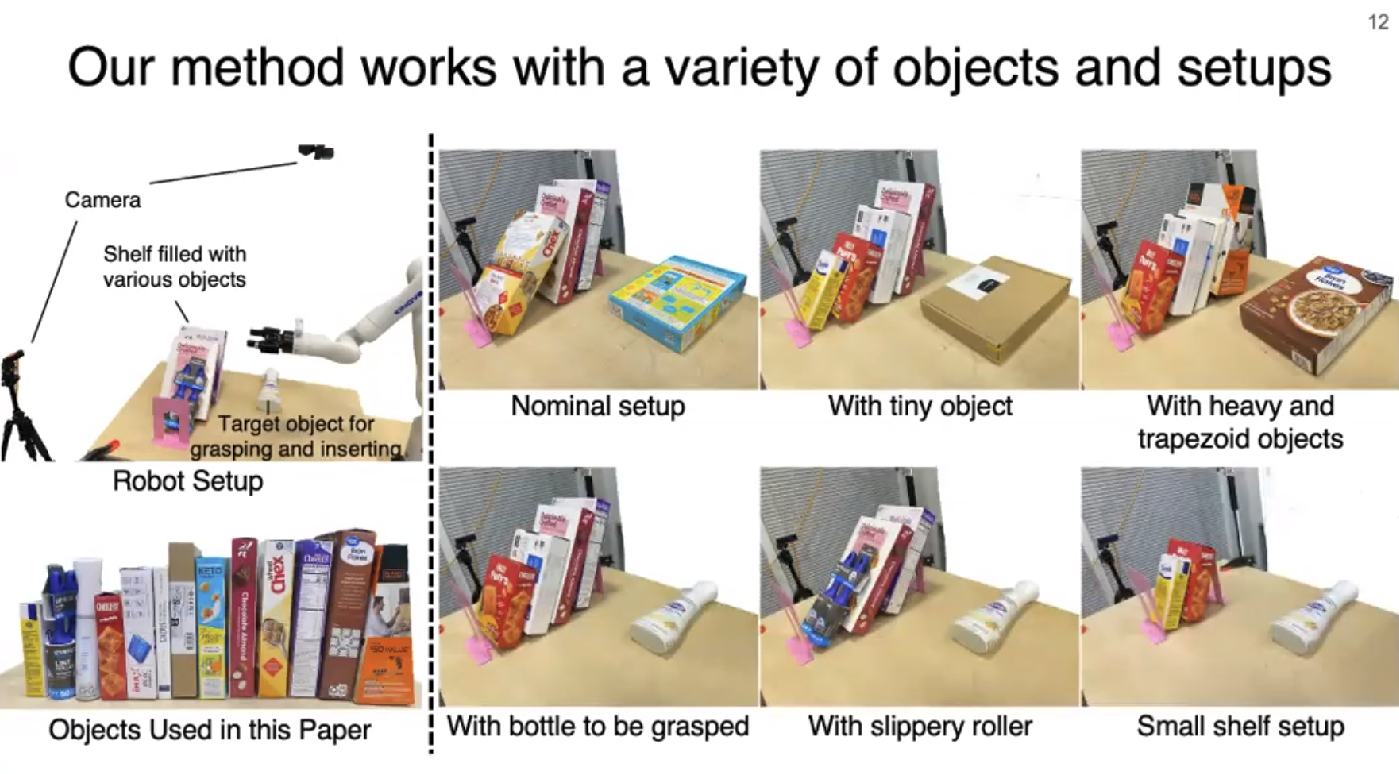
Fig. 5: Experimental Setup.

각 Action primitive 마다 300개의 episode dataset을 구축함. (각 skill에 따른 key pose도 포함됨.)
shelf width로 randomization을 주었다. 그리고 shelf에 꽂힌 물체의 갯수/property/size/density에 대해서도 randomization을 수행했다.
Kinova Gen3 Robot + OAK-D camera
Evaluation metrics
- Mean Squared Error (MSE)
- Earth Mover’s Distance (EMD)
- Chamfer distance (CD)

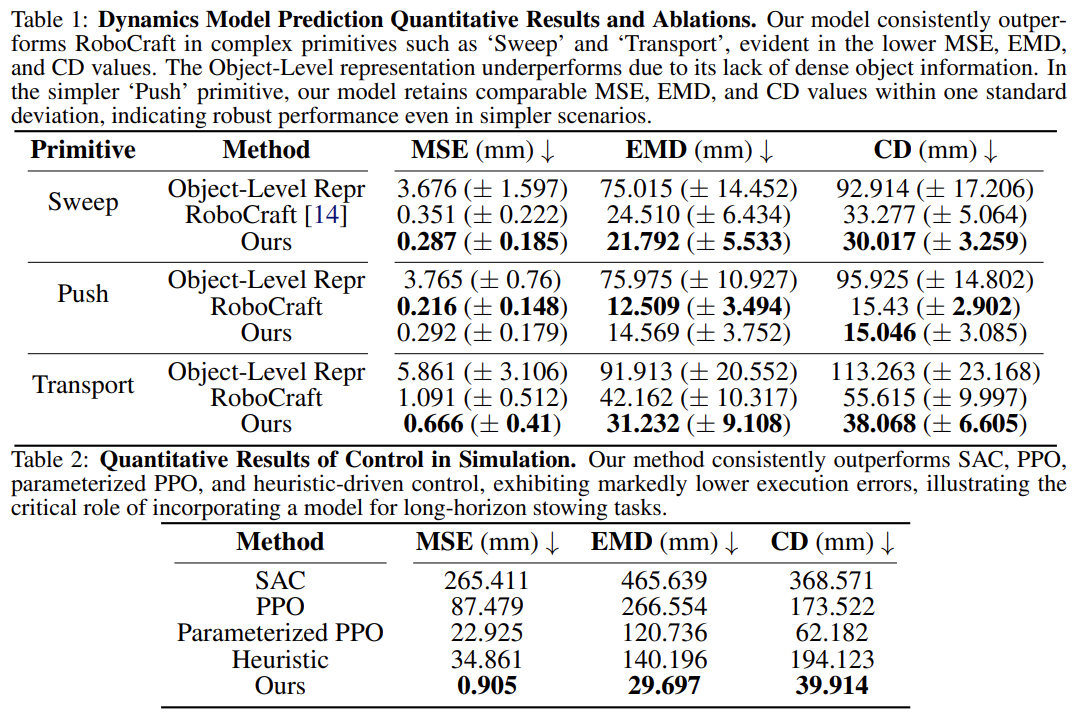
Fig. 6: Results about STOW-GNN.

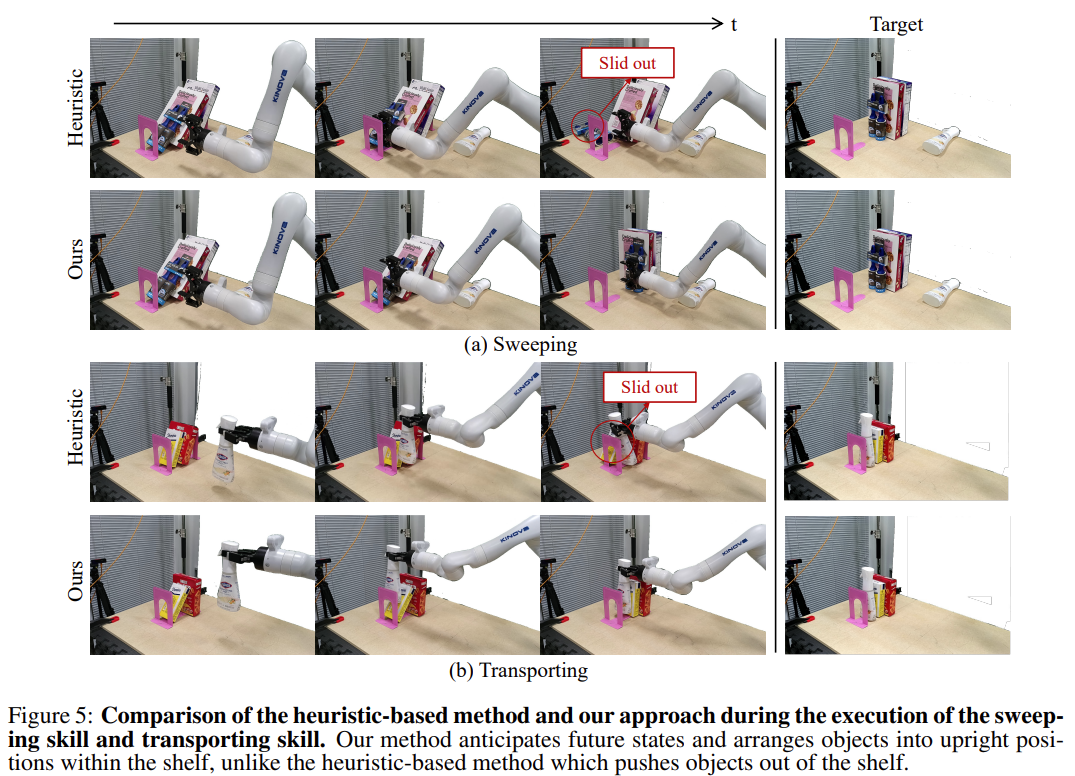
Fig. 7: Still-cut about STOW-GNN.

Thought

Shelf, Cluttered env에서 수행하는 pick-n-place를 stowing task라고 표현하는 것을 처음 알게 되었습니다.
GNN 으로 rigid body dynamics를 예측하고 (정확히는 state(pose)를 예측하고), 이 예측값에 가장 근접하는 action primitive \(a_{p}\)를 찾는 연구입니다. 논문에서는 rigid body에 대해 모두 box shape의 point-cloud particle로 정의했는데, 다른 형태의 물체에 대해서는 실험을 수행하지 않은 점이 궁금합니다.
해당 논문에서 보여준 transporting task는 꽤 괜찮은 task인 것 같습니다.

한계점

manual human labeling of ordered keyframes from demonstration
used box-shaped point clouds to represent objects